Topocentrische plaatsbepaling
Vragenrubriek, verschenen in Urania jg. 88 nr. 1, 1994, p.19
Reeds enige jaren gebruikt de Werkgemeenschap van Astrologen (WvA) voor de horoscopen in Urania een berekeningswijze voor de planeetplaatsen die afwijkt van de berekeningswijze zoals we die meestal met de hand of de rekenmachine uitvoeren, en zoals we die in de STOA basiscursus leren [leerdern in 1994]. Sinds de WvA voor de berekeningen van horoscopen de beschikking heeft over het computerprogramma Scorpio van Joost ter Laak is het mogelijk geworden in plaats van met geocentrische planeetplaatsen, te werken met de zogenaamde topocentrische planeetplaatsen. Naar aanleiding van een ingezonden brief van de heer F. van Lent uit Apeldoorn wil ik graag een aantal punten met betrekking tot dit onderwerp op een rijtje zetten en de bevindingen van Dhr. van Lent aan u voorleggen.
Allereerst een korte weergave van de twee systemen. We kunnen deze twee verschillende opvattingen als volgt kort definieren: De topocentrische positie van een hemellichaam is de positie van het hemellichaam gezien vanuit de plaats van waarneming. (Gr. topos=plaats) De geocentrische positie van een hemellichaam is de plaats van het hemellichaam gezien vanuit het middelpunt van de aarde. Deze geocentrische posities zijn de posities zoals ze in de ephemeride staan. In zijn artikel "Geocentrische of topocentrische posities?" in Urania gaat Joost ter Laak uitgebreid in op de theorie van de topocentrische planeetplaatsen. [1]
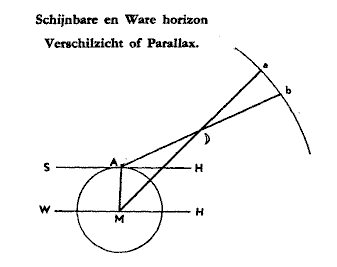
M = het middelpunt van de aarde, het geocentrum
A = plaats van waarneming op het aardoppervlak, het topocentrum, b.v. de geboorteplaats
SH = schijnbare horizon
WH = ware horizon
a = geocentrische positie van de Maan
b = topocentrische positie van de Maan
(figuur overgenomen uit "Het mysterie van ons lot en leven" [3])
In de tijd waarin de grondslagen van de WvA berekeningstechniek werden gevormd is dit onderwerp ook al eens aan de orde geweest. In het Kringblad van de Astrologische Kring van het NAG werd in 1936 door de heer P.F. van Solt de volledige berekening van de topocentrische plaatsbepaling gegeven. [2] Het artikel mondde uit in een reeks stellingen. Uitgangspunt was hierbij dat astrologen de positie van de hemellichamen willen vastleggen ten opzichte van de plaats van waarneming. In het artikel wordt de mogelijkheid aangegeven om het "vlak van beschouwing te verleggen (van het middelpunt van de aarde (I.)) naar het oppervlak van de aarde" en de lezers aangemoedigd met de topocentrische posities aan de gang te gaan. Echter in die tijd was de berekening zoals die in het artikel beschreven werd een niet te onderschatten obstakel voor diegenen die niet begiftigd waren met een grote liefde voor rekenlineaal en logaritmentabel. Weliswaar wordt in het artikel nog geen standpunt ingenomen voor of tegen het gebruik van topocentrische posities.
Leo Knegt spreekt zich vervolgens in zijn boek "Het mysterie van ons lot en leven" nadrukkelijk uit tegen het gebruik van de topocentrische planeetplaatsen. [3] Hij vindt dat alle geometrische verhoudingen voor het centrum van de aarde hetzelfde zijn als voor de plaatselijke hemelsfeer en dat daarom de geocentrische positie gebruikt moet worden. Daarna argumenteert hij dat omdat wij de geocentrische positie dienen te gebruiken, we niets te maken hebben met de topocentrische posities. Aldus een verkorte weergave van zijn redenering.
Th.J.J. Ram neemt op zeker moment ook een standpunt in in de discussie. [4] Hij vindt op zijn beurt dat het topocentrische standpunt het meest individuele is, en daarom te verkiezen boven het geocentrische. We hebben het immers over de horoscoop als een unieke weergave van de kosmische situatie op een bepaalde plaats en tijd op het aardoppervlak. Een momentopname die gebonden is aan een waarnemer als subject ten opzichte van de kosmische invloeden. Deze waarnemer is het middelpunt van zijn individuele sfeer. Deze sfeer kunnen we vergelijken met de aura van de mens. Dit perspectief is dus topocentrisch.
De topocentrische plaatsbepaling wordt verder in de astrologische wereld meestal gebruikt onder de naam "parallaxcorrectie". In moderne computerprogramma's wordt meestal de keuze gegeven de parallaxcorrectie al dan niet toe te passen. Vaak ook wordt alleen voor de berekening van de Maanstand deze mogelijkheid geboden, omdat bij de Maan de afwijking verhoudingsgewijs het grootst is.
Tot zover enkele inleidende opmerkingen. De brief die de heer F. van Lent onlangs aan de redactie stuurde bevat het verslag van een onderzoekje dat hij verrichtte om te achterhalen welke berekeningswijze voor de positie van de Maan de "juiste" zou zijn. Met het begrip "juiste berekeningswijze" bedoelt hij dan die berekeningswijze waarvan het resultaat het meest met de waarneming overeenkomt, in die zin dat de op- en ondergangstijd van de Maan overeenkomt met het moment dat de Maan conjunct met de ascendant, respectievelijk conjunct met de descendant staat. Uit het onderzoekje van de heer Van Lent blijkt dat de geocentrische positie van de Maan beter overeenkomt met de waargenomen positie dan de topocentrische positie. Dit is uiteraard zeer verbazingwekkend. Volgens het bovenstaande beeld moet juist de topocentrische Maan bij opkomst en ondergang exact op de horizon van de plaats van waarneming staan.
De tijden van op- en ondergang die voor astronomische doeleinden gebruikt worden zijn meestal letterlijk de tijdstippen waarop het eerste streepje maanlicht boven de horizon verschijnt respectievelijk helemaal eronder verdwenen is. De conjunctie met de ascendant, respectievelijk descendant, zoals die door astrologen wordt gehanteerd, vindt plaats op het moment dat het midden van de maanschijf precies op de horizon staat. De gehele doorsnede van de maanschijf bedraagt ongeveer 32 boogminuten hetgeen overeenkomt met een verschil in tijd tussen de conjunctie met de horizon en het op- of ondergaan van de Maan van maximaal ongeveer 1,7 minuten op onze geografische breedte.
Daarnaast is de refractie, dat wil zeggen de breking van het licht in de dampkring, er de oorzaak van dat wij meestal de Maan boven de horizon zien staan terwijl hij in werkelijkheid nog moet opkomen, of reeds ondergegaan is. Dit verschijnsel kan een vrij grote afwijking geven ten opzichte van de berekende positie van de Maan, namelijk ongeveer gemiddeld 34 boogminuten wanneer de Maan in de buurt van de horizon staat, hetgeen in tijd overeenkomt met bijna vier minuten. De refractie van de atmosfeer kan nogal verschillen bij verschillende weertypen. Bij een hoge temperatuur en een lage luchtdruk kan de refractie tot 7 boogminuten kleiner zijn dan gemiddeld. Astrologen, in tegenstelling tot astronomen, gebruiken meestal geen refractie bij hun berekeningen. Ik zou me ook eerlijk gezegd niet zo goed kunnen voorstellen dat ik, om te bepalen of iemand de Maan in sector 1 of in sector 12 heeft, moest gaan nazoeken of het op die dag misschien regende, omdat de Maan dan misschien nog net in sector 12 zou kunnen staan. De astrologische invloed van de hemellichamen werkt wellicht niet zo, dat ze als een lichtstraal tot ons komt en aan dezelfde fysische wetten voldoet als het licht. Dit roept overigens wel de vraag op waar we nu eigenlijk een horoscooptekening van maken: van de kosmische toestand zoals die zich visueel aan ons voordoet aan de hemel, of van de kosmische toestand zoals die wiskundig gezien is.
Verder kan nog in aanmerking genomen worden de zogenaamde "kimduiking". Hoe hoger de waarnemer zich boven het zeeniveau bevindt hoe eerder hij een hemellichaam boven de horizon ziet verschijnen. De correctie voor dit verschijnsel bedraagt hoogstens enige boogminuten.
Als we deze afwijkingen allemaal optellen bij de astrologische stand moeten we kunnen zien dat inderdaad het "astronomische" moment van opkomst van de Maan overeenkomt met het moment van de conjunctie van de topocentrische Maan met de ascendant.
Een voorbeeld uit de brief van Dhr. van Lent. De ondergang van de Maan op 9 februari 1993 te Utrecht, 52°05'NB, 5°08' OL vindt plaats om 8 uur 38 MET. De met het programma Scorpio met ware plaats berekende geocentrische Maan staat dan op 4°49' Maagd. De descendant is op dat moment 4°2' Maagd, een verschil van 41'. Dit verschil zou wellicht verklaard kunnen worden uit de bovengenoemde afwijkingen. De met ware plaats berekende topocentrische Maan staat op dat moment op 1°12' Maagd. Dit is een verschil van -3°47' met de descendant. Passen we vervolgens nog de bovengenoemde correcties toe: diameter maan + refractie + kimduiking = +16' + 34' + 0' = +50'. De standhoek van de ecliptica in aanmerking genomen wordt dit verschil ongeveer +56' in lengte. Dit levert:
geocentrisch: 41' + 56' = 1°39' verschil met descendant
topocentrisch: -3°47' + 56' = -2°51' verschil met descendant.
We zien hier dat de door het programma Scorpio berekende topocentrische Maan helemaal niet conjunct met de descendant staat. De geocentrische Maan klopt zelfs beter, zoals Dhr. van Lent ook constateerde. Dan kan nog worden nagegaan of de gegeven tijden van opkomst en ondergang misschien onnauwkeurig zijn, of dat ze misschien niet datgene weergeven wat wij hier onder op- en ondergang verstaan.
Ter controle nog een voorbeeld uit de Nautical Almanac. [5] De tijd van opkomst van de Maan op 18 oktober 1972 op 52°0'NB, 0°0' OL is 15 uur 3 minuten GMT. Op dit moment vinden we een ascendant van 21°26' Waterman. De geocentrische Maan met ware plaats staat 21°12' Waterman, een verschil van 14'. De topocentrische Maan met ware plaats staat 24°24' Waterman, een verschil van 2°58'. In de Nautical Almanac zijn de gemiddelde refractie en de diameter van de maanschijf verdisconteerd zodat we nog de correcties erbij moeten optellen, respectievelijk aftrekken, om te kunnen zien of de topocentrische Maan al dan niet conjunct met de ascendant staat. De correcties zijn bijelkaar ongeveer 50 boogminuten. Geprojecteerd op de ecliptica wordt dit verschil ongeveer 2°42'. Omdat we hier met een opkomst te maken hebben moeten we de correctie in anti-zodiakale richting toepassen. Dit levert een verschil met de ascendant op van, voor de geocentrische Maan 2°56', en voor de topocentrische Maan 0°15'. Deze laatste komt dus aardig dicht in de buurt van de ascendant. Zonder de correcties toe te passen lijkt het misschien alsof de geocentrische Maan dichter bij de ascendant komt, maar door de correcties toe te passen blijkt dat de topocentrische Maan veel beter klopt.
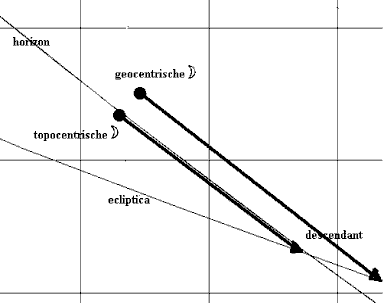
Na vervolgens een reeks steekproeven te hebben genomen met behulp van de op- en ondergangstijden uit de Nautical Almanac bleek dat, geheel conform het hierboven beschreven idee, steeds de topocentrische positie van de Maan zeer dicht bij de ascendant kwam te staan. De onnauwkeurigheid die ik vond lag gemiddeld rond de 10', en is wellicht te wijten aan de onnauwkeurigheid van mijn eigen berekeningswijze. Wat betreft de op- en ondergangstijden die Dhr. van Lent gebruikte voor zijn onderzoekje moeten we veronderstellen dat ze in elk geval niet uit de Nautical Almanac zijn overgenomen, en dat berekeningen op basis van deze gegevens niet tot het te verwachten resultaat leiden.
Met als uitgangspunt de op- en ondergangstijden uit de Nautical Almanac, en na toepassing van de verschillende correcties kunnen we zien dat de topocentrische Maan (met ware plaats), zoals die in Urania gebruikt wordt, inderdaad die Maan is die bij opkomst op de ascendant staat en bij ondergang op de descendant. En juist daarom is deze Maan mijns inziens voor astrologen de meest geeigende om te gebruiken bij het berekenen van horoscoop. 
Noten
1. Joost ter Laak, "Geocentrische of topocentrische posities?", in Urania, Oktober 1990
2. P.F.van Solt, "Geografische, geocentrische, of topocentrische plaatsbepaling in verband met de astrologie", Kringblad van de Astrologische Kring van het N.A.G., April 1936
3. Leo Knegt, "Het mysterie van ons lot en leven", uitg. Spin & Zoon N.V., Amsterdam, tweede druk, blz. 139 e.v.
4. Th.J.J.Ram, "Plaats en Tijd", Kringblad van de Astrologische Kring van het N.A.G., Mei 1936
5. "Nautical Almanac" 1972, UK edition, 1970
Bekijk ook de website van de Werkgemeenschap van Astrologen.